Exploring Recipes dataset via Random Forest

Name(s): Xiangzhi Jiang (xzjiang@umich.edu)

Step 1: Introduction

Core Question: Can we predict how well a recipe will be rated — before any user has rated it — using only basic information like preparation time, complexity, and tags?

In this project, we focus on forecasting the average rating of each recipe on Food.com using only metadata available prior to any user interaction. This includes numeric features that reflect preparation effort, and categorical tags that capture recipe themes or constraints (e.g., “vegan”, “holiday”, “easy”).

Why this matters:

Datasets

We use two datasets:

Task Setup

This is a regression task. The response variable is the average rating per recipe, calculated from the RAW_interactions.csv data.

We limit our model to four features:

Feature Type Description
minutes Quantitative Total time (in minutes) to prepare the recipe
n_steps Quantitative Number of procedural steps — a proxy for recipe complexity
n_ingredients Quantitative Count of distinct ingredients used
tags Categorical List of user-assigned labels — dietary, cultural, seasonal, or topical

These features were selected because they are:

Step 2: Data Cleaning and Exploratory Data Analysis

Cleaning Steps and Rationale

  1. Merge Datasets
    We join the recipe metadata with user interactions using the recipe ID. This allows us to associate each recipe with its user ratings.

  2. Replace Zero Ratings
    Ratings of 0 are treated as invalid or missing, and are replaced with NaN. They may arise from submission errors or default placeholders.

  3. Compute Average Rating
    We aggregate individual user ratings to create a per-recipe average — our target variable. This is the value we aim to predict.

  4. Quantile Trimming
    We remove outliers in the quantitative features (minutes, n_ingredients, n_steps) by trimming to the 2.5–97.5 percentile range. This reduces skew and improves model stability.

Visual Explorations

⏱️ Average Rating vs. Cooking Time

Figure 1: Rating vs. Duration

We observe that recipes under 100 minutes tend to have a wider spread of ratings, but overall the average rating remains relatively stable. However, some long-duration recipes receive lower ratings, hinting that minutes may capture subtle user frustration or expectation mismatches.

🪜 Average Rating by Number of Steps

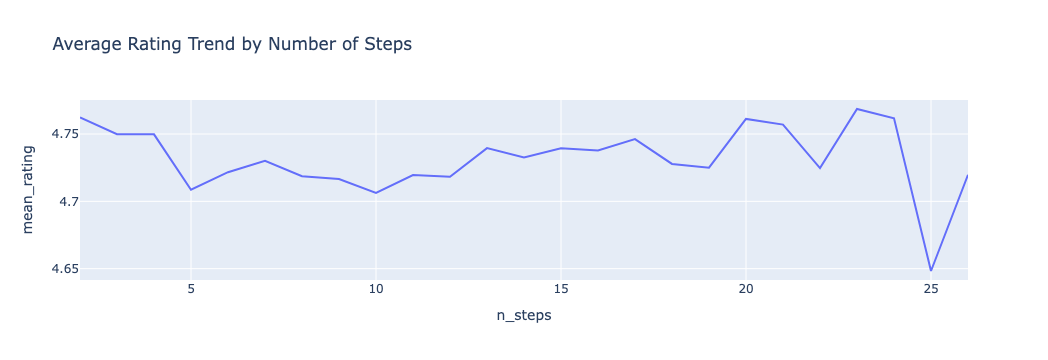
Figure 2: Rating vs. Steps

This plot reveals that highly complex recipes (with more than 20 steps) slightly trend toward higher ratings, suggesting that advanced users may appreciate detailed guidance. However, the overall variation is subtle and nonlinear — supporting later use of feature engineering like steps_per_ing.

⭐ Distribution of Average Ratings

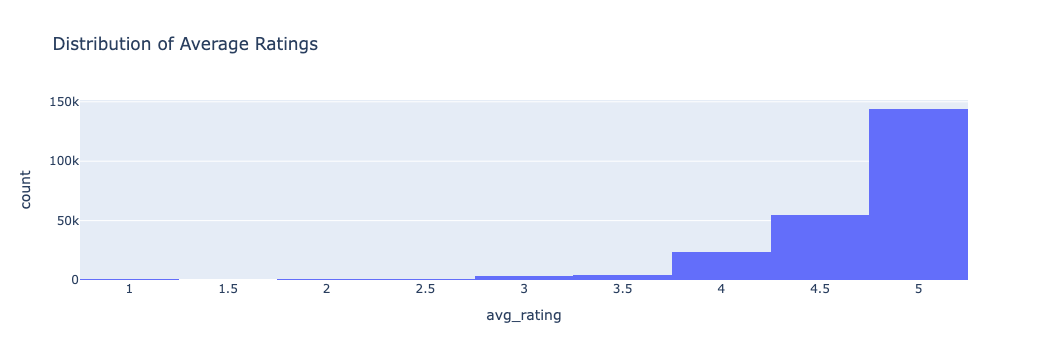
Figure 3: Average Rating Histogram

The average ratings are heavily right-skewed, with most clustered between 4.5 and 5. This distribution suggests user generosity or rating inflation — an important contextual factor when interpreting model performance.

merged = pd.merge(recipes, interactions, how="left", left_on="id", right_on="recipe_id")
merged["rating"] = merged["rating"].replace(0, np.nan)

avg_rating = merged.groupby("id")["rating"].mean()
merged["avg_rating"] = merged["id"].map(avg_rating)
merged["nutrition"] = merged["nutrition"].apply(eval)
nutrition_cols = ["calories", "total_fat", "sugar", "sodium", "protein", "saturated_fat", "carbohydrates"]
for i, col in enumerate(nutrition_cols):
    merged[col] = merged["nutrition"].apply(lambda x: x[i] if isinstance(x, list) and len(x) > i else np.nan)

merged["submitted"] = pd.to_datetime(merged["submitted"])
merged["date"] = pd.to_datetime(merged["date"], errors='coerce')

q_minutes = merged["minutes"].quantile([0.025, 0.975])
q_ingredients = merged["n_ingredients"].quantile([0.025, 0.975])
q_steps = merged["n_steps"].quantile([0.025, 0.975])
q_rating = merged["avg_rating"].quantile([0.025, 0.975])

filtered = merged[
    (merged["minutes"] >= q_minutes[0.025]) & (merged["minutes"] <= q_minutes[0.975]) &
    (merged["n_ingredients"] >= q_ingredients[0.025]) & (merged["n_ingredients"] <= q_ingredients[0.975]) &
    (merged["n_steps"] >= q_steps[0.025]) & (merged["n_steps"] <= q_steps[0.975]) &
    (merged["avg_rating"] >= q_rating[0.025]) & (merged["avg_rating"] <= q_rating[0.975])
].copy()


fig1 = px.histogram(merged, x="avg_rating", nbins=20, title="Distribution of Average Ratings")
fig1.show()

fig2 = px.scatter(filtered, x="minutes", y="avg_rating",
                  title="Average Rating vs. Cooking Time (Filtered)",
                  opacity=0.5, trendline="ols")
fig2.show()

bar_df = filtered.groupby("n_ingredients").agg(
    mean_rating=("avg_rating", "mean"),
    count=("avg_rating", "count")
).reset_index()


line_df = filtered.groupby("n_steps").agg(mean_rating=("avg_rating", "mean")).reset_index()

fig4 = px.line(line_df, x="n_steps", y="mean_rating",
               title="Average Rating Trend by Number of Steps")
fig4.show()

grouped = merged.groupby("n_ingredients")["avg_rating"].agg(["count", "mean"]).reset_index()
grouped.columns = ["n_ingredients", "num_recipes", "mean_avg_rating"]
grouped_sorted = grouped.sort_values(by="n_ingredients")

grouped_sorted.head(10)

merged["avg_rating_filled"] = merged["avg_rating"].fillna(merged["avg_rating"].mean())

Step 3: Defining the Prediction Task

🎯 Prediction Target: avg_rating

We compute the average rating for each recipe from all available user interactions. This rating is bounded between 1 and 5 and serves as the ground truth for our regression model.

✅ Justification for Feature Usage

All four input features were chosen because they are:

Feature Reason for Inclusion
minutes Longer or very short prep times may affect user satisfaction
n_steps Captures procedural complexity — longer instructions might deter or attract users
n_ingredients Reflects how resource-intensive a recipe is
tags Encodes important categorical signals such as dietary restrictions or seasonal usage

📏 Evaluation Metrics

To evaluate the quality of our model, we use:

Step 4: Baseline Model

To build a simple and interpretable reference model, we start with a linear regression using four original features:

Preprocessing

We applied the following preprocessing pipeline:

model_df = filtered[["minutes", "n_steps", "n_ingredients", "tags", "avg_rating"]].dropna()

X = model_df.drop(columns=["avg_rating"])
y = model_df["avg_rating"]

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

def simplify_tags(tag_str):
    try:
        tags = eval(tag_str)
        return tags[0] if isinstance(tags, list) and tags else "unknown"
    except:
        return "unknown"

X_train["tags"] = X_train["tags"].apply(simplify_tags)
X_test["tags"] = X_test["tags"].apply(simplify_tags)

numeric_features = ["minutes", "n_steps", "n_ingredients"]
categorical_features = ["tags"]

preprocessor = ColumnTransformer(transformers=[
    ("num", StandardScaler(), numeric_features),
    ("cat", OneHotEncoder(handle_unknown="ignore"), categorical_features)
])

baseline_model = Pipeline(steps=[
    ("preprocessor", preprocessor),
    ("regressor", LinearRegression())
])

baseline_model.fit(X_train, y_train)
y_pred = baseline_model.predict(X_test)

mse = mean_squared_error(y_test, y_pred)
r2 = r2_score(y_test, y_pred)

print("Baseline Linear Regression Results (4 original features):")
print(f"  MSE: {mse:.4f}")
print(f"  R^2: {r2:.4f}")

Step 5: Final Model with Feature Engineering

To enhance the model’s expressiveness and capture more nuanced structure in the data, we engineer the following new features:

These derived features aim to capture nonlinear interactions between effort, complexity, and recipe structure. The categorical tags column is still simplified to its first tag and one-hot encoded. We use a Random Forest Regressor with hyperparameter tuning via GridSearchCV to handle nonlinearity and categorical splits efficiently.

model_df = filtered[["minutes", "n_steps", "n_ingredients", "tags", "avg_rating"]].dropna()
model_df["log_minutes"] = np.log1p(model_df["minutes"])
model_df["step_density"] = model_df["n_steps"] / model_df["minutes"].replace(0, np.nan)
model_df["ingredient_density"] = model_df["n_ingredients"] / model_df["minutes"].replace(0, np.nan)
model_df["steps_per_ing"] = model_df["n_steps"] / model_df["n_ingredients"].replace(0, np.nan)

feature_cols = ["log_minutes", "step_density", "ingredient_density", "steps_per_ing", "tags"]
X = model_df[feature_cols]
y = model_df["avg_rating"]

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

def simplify_tags(tag_str):
    try:
        tags = eval(tag_str)
        return tags[0] if isinstance(tags, list) and tags else "unknown"
    except:
        return "unknown"

X_train["tags"] = X_train["tags"].apply(simplify_tags)
X_test["tags"] = X_test["tags"].apply(simplify_tags)

numeric_features = ["log_minutes", "step_density", "ingredient_density", "steps_per_ing"]
categorical_features = ["tags"]

preprocessor = ColumnTransformer(transformers=[
    ("num", StandardScaler(), numeric_features),
    ("cat", OneHotEncoder(handle_unknown="ignore"), categorical_features)
])

final_pipeline = Pipeline(steps=[
    ("preprocessor", preprocessor),
    ("regressor", RandomForestRegressor(random_state=42))
])

param_grid = {
    "regressor__n_estimators": [100, 200],
    "regressor__max_depth": [5, 10, 15],
    "regressor__min_samples_split": [2, 5]
}

total_combinations = len(ParameterGrid(param_grid))
print(f"🔧 Total grid combinations: {total_combinations}")

start_time = time.time()

grid_search = GridSearchCV(
    final_pipeline,
    param_grid,
    cv=3,
    scoring="neg_mean_squared_error",
    n_jobs=-1,
    verbose=2
)
grid_search.fit(X_train, y_train)

end_time = time.time()
duration = end_time - start_time
print(f"\n⏱️ Total training time: {duration:.2f} seconds")

y_pred = grid_search.best_estimator_.predict(X_test)
mse = mean_squared_error(y_test, y_pred)
r2 = r2_score(y_test, y_pred)

print("\n Final Model: Random Forest with 4 Engineered Features")
print(f"Best Params: {grid_search.best_params_}")
print(f"MSE: {mse:.4f}")
print(f"R²: {r2:.4f}")

Conclusion

This project explored how simple metadata from Food.com recipes — including time, ingredients, and tags — can be used to predict average user ratings before any reviews are submitted.

We began with a baseline linear regression using raw features. While interpretable and efficient, its performance was limited:

The low R² value suggests that the linear model explained very little variance in the target, likely due to:

To address these limitations, we engineered four domain-informed features: We then used a Random Forest Regressor, which yielded notable gains:

Why Random Forest?

Random Forests are well-suited for this task because:

Despite the modest R², the observed improvement over the linear baseline confirms that more expressive models and thoughtfully engineered features can extract additional structure from even simple recipe metadata. Future work could incorporate textual reviews or image embeddings to further boost performance.